피어슨상관계수의 표준오차
1.1. 집단간분산과 집단내분산
1. 애니메이션
2. 설명
2.1. 양적 확률변수의 모수와 표본통계량의 추정량(estimator)
양적 확률변수 $X$를 가지는 개체로 이루어진 집단의 추정량(estimator)
$X$의 모평균 : $\mu_{X}$
$$\mu_{X} = \dfrac{\sum\limits_{i=1}^{N}X_i}{N}$$
여기서, $N$은 집단크기 : 무한집단인 경우 $N → ∞$
$X$의 표본평균 : $\bar {X}$
$$\bar {X} =\dfrac{\sum\limits_{i=1}^{n}X_i}{n}$$
여기서, $n$은 표본크기
$X$의 모분산 : $\sigma^2_{X}$
$$\sigma^2_{X} = \dfrac{\sum\limits_{i=1}^{N}(X_i – \mu_X)^2}{N}$$
여기서, $\mu_X$는 확률변수 $X$의 모평균
$N$은 집단크기 : 무한집단인 경우 $N → ∞$
$X$의 표본분산 : $S^2_{X}$
$$S^2_{X} = \dfrac{\sum\limits_{i=1}^{n}(X_i{-}\bar{X})^2}{n-1}$$
여기서, $\bar{X}$는 확률변수 $X$의 표본평균
$n$은 표본크기
$X$의 모표준편차 : $\sigma_{X}$
$$\sigma_{X} = \sqrt{\dfrac{\sum\limits_{i=1}^{N}(X_i – \mu_X)^2}{N}}$$
여기서, $\mu_X$는 확률변수 $X$의 모평균
$N$은 집단크기 : 무한집단인 경우 $N → ∞$
$X$의 표본표준편차 : $S_{X}$
$$S_{X} = \sqrt{\dfrac{\sum\limits_{i=1}^{n}(X_i{-}\bar{X})^2}{n-1}}$$
여기서, $\bar{X}$는 확률변수 $Y$의 표본평균
$n$은 표본크기
양적 확률변수 $Y$를 가지는 개체로 이루어진 집단의 추정량(estimator)
$Y$의 모평균 : $\mu_{Y}$
$$\mu_{Y} = \dfrac{\sum\limits_{i=1}^{N}Y_i}{N}$$
여기서, $N$은 집단크기 : 무한집단인 경우 $N → ∞$
$Y$의 표본평균 : $\bar {Y}$
$$\bar {Y} =\dfrac{\sum\limits_{i=1}^{n}Y_i}{n}$$
여기서, $n$은 표본크기
$Y$의 모분산 : $\sigma^2_{X}$
$$\sigma^2_{Y} = \dfrac{\sum\limits_{i=1}^{N}(Y_i – \mu_Y)^2}{N}$$
여기서, $\mu_Y$는 확률변수 $Y$의 모평균
$N$은 집단크기 : 무한집단인 경우 $N → ∞$
$Y$의 표본분산 : $S^2_{Y}$
$$S^2_{Y} = \dfrac{\sum\limits_{i=1}^{n}(Y_i{-}\bar{Y})^2}{n-1}$$
여기서, $\bar{Y}$는 확률변수 $Y$의 표본평균
$n$은 표본크기
$Y$의 모표준편차 : $\sigma_{Y}$
$$\sigma_{Y} = \sqrt{\dfrac{\sum\limits_{i=1}^{N}(Y_i{-}\mu_{Y})^2}{N}}$$
여기서, $\mu_{Y}$는 확률변수 $Y$의 모평균
$N$은 집단크기 : 무한집단인 경우 $N → ∞$
$Y$의 표본표준편차 : $S_Y$
$$S_{Y} = \sqrt{\dfrac{\sum\limits_{i=1}^{n}(Y_i{-}\bar{Y})^2}{n-1}}$$
여기서, $\bar{Y}$는 확률변수 $Y$의 표본평균
$n$은 표본크기
양적 확률변수 $X$와 $Y$를 가지는 개체로 이루어진 집단의 추정량(estimator)
모공분산 : 모$\mathrm{Cov}(X{,}Y)=\sigma_{XY}$
$$\sigma_{XY}=\dfrac{\sum\limits_{i=1}\limits^{N}(X_i{-}\mu_{X})(Y_i{-}\mu_{Y})}{N}$$
여기서, $\mu_{X}$는 확률변수 $X$의 모평균
$\mu_{Y}$는 확률변수 $Y$의 모평균
$N$은 집단크기 : 무한집단인 경우 $N → ∞$
표본공분산 : 표본$\mathrm{Cov}(X{,}Y)=S_{XY}$
$$S_{XY}=\dfrac{\sum\limits_{i=1}\limits^{n}(X_i{-}\bar{X})(Y_i{-}\bar{Y})}{n-1}$$
여기서, $\bar{X}$는 확률변수 $X$의 표본평균
$\bar{Y}$는 확률변수 $Y$의 표본평균
$n$은 표본크기
모피어슨상관계수
$$\rho_{XY}=\dfrac {\sigma_{XY}} {\sigma_{X}\sigma_{Y}}=\dfrac{\dfrac{\sum\limits_{i=1}^{N}(X_i-\mu_X)(Y_i-\mu_Y)}{N}} {\sqrt{\dfrac{\sum\limits_{i=1}^{N}(X_i-\mu_X)^2}{N}}\sqrt{\dfrac{\sum\limits_{i=1}^{N}(Y_i-\mu_Y)^2}{N}}}$$
여기서, $\sigma_{XY}$는 $X$와 $Y$의 모공분산
$\sigma_{X}$는 $X$의 모표준편차
$\sigma_{Y}$는 $Y$의 모표준편차
$\mu_{X}$는 $X$의 모평균
$\mu_{Y}$는 $Y$의 모평균
$N$은 집단크기 : 무한집단인 경우, $N → ∞$
표본피어슨상관계수
$${r}_{XY}=\dfrac {S_{XY}} {S_{X}S_{Y}}=\dfrac{\dfrac{\sum\limits_{i=1}^{n}(X_i-\bar X)(Y_i-\bar Y)}{n-1}} {\sqrt{\dfrac{\sum\limits_{i=1}^{n}(X_i-\bar X)^2}{n-1}}\sqrt{\dfrac{\sum\limits_{i=1}^{n}(Y_i-\bar Y)^2}{n-1}}}$$
여기서, $S_{XY}$는 $X$와 $Y$의 표본공분산
$S_X$는 $X$의 표본표준편차
$S_Y$는 $Y$의 표본표준편차
$\bar X$는 $X$의 표본평균
$\bar Y$는 $Y$의 표본평균
$n$은 표본크기
2.2. 상관(correlation)
개체(object, 요소, element)가 두 변수를 가지고 두 변수가 서로 독립적이라면 2차원 직교좌표계에 개체를 점(point)로 표시할 수 있습니다. 개체에서 관측된 두 변수값은 점의 좌표가 됩니다. 개체가 이루는 집단을 좌표계에 점들로 표현한 것을 그 집단의 산점도라 합니다. 산점도를 통해서 개체가 이루는 집단의 분포를 볼 수 있고 더욱 더 중요한 것은 개체가 가지는 변수 간의 상관(서로 간의 관계)의 정도를 볼 수 있다는 것입니다. 예를 들면 개체가 가지는 두 변수의 상관관계를 보고자 할때 개체가 이루는 집단의 2차원 산점도(scatter plot)를 그립니다. 만일 산점도의 점들이 평균점을 중심으로 방사형으로 고르게 나타나거나 점들이 축과 평행하게 분포한다면 두 변수는 상관이 없다고 할 수 있습니다. 즉, 평균점을 기준으로 방향이 랜덤하거나 평균점에서 좌표축과 평행하게 나타난다는 것은 모두 고정되어 있는 두 평균만 관계가 있다고 볼 수 있습니다. 즉 상관이 있다는 것은 한 변수가 변화할 때 다른 변수가 일정한 규칙으로 변화한다는 것을 의미합니다.
상관의 시각화
– 한 변수의 자기상관(auto correlation) : 2차원 산점도에서 한 직선상에 분포합니다.
– 두 변수의 상관(correlation) : 두 변수를 좌표축으로 하는 2차원 산점도를 그려서 시각화합니다.
– 공유된 한 변수(종속변수)와 여러 변수(독립변수)가 각기 이루는 상관 : 공유된 한 변수를 한 좌표축으로 하고 그 축에서의 독립변수들의 절편을 같게 한 직교좌표계에 독립변수 수 만큼의 2차원 산점도를 그려서 시각화합니다.
– 여러 변수의 상관 : 2차원 산점도를 원소로 하는 자기상관행렬(auto correlation matrix)을 그려서 시각화합니다.
상관분석
상관분석(correlation analysis)는 두 변수 간의 선형적인 관계의 정도를 분석합니다. 예를 들면 한 변수의 증가분에 비례하여 다른 변수가 증가 또는 감소하는 가를 분석하는 것입니다. 만일 두 변수값이 종모양의 확률분포를 가지는 확률변수에서 실현된 변수값이라고 한다면, 점들의 분포가 원형분포에서 타원형분포로 더나아가 직선으로 분포하는 것은 점점 상관이 커지고 있다고 말할 수 있습니다. 이 정도를 수치화하는 방법에는 피어슨 상관계수가 있습니다. 피어슨 상관계수는 마이너스 1부터 플러스 1까지 숫자로 나타납니다.
두 확률변수가 종모양의 확률분포를 가지고 있다는 것은 두 확률변수가 평균으로의 회귀성을 가지고 있다고 볼 수 있습니다. 한 변수가 증가할 때 다른 변수가 비례하여 얼마나 선형적으로 증가 또는 감소를 하는가를 선형의 상관의 정도라고 할 수 있고 회귀성(중심으로 돌아가려는 성질)이 있다고도 할 수 있습니다. 따라서 상관의 정도를 나타내는 제곱하여 항상 부호가 양수가 되는 상관계수의 제곱은 회귀의 정도를 나타내는 결정계수가 됩니다. 상관계수는 두 변수가 증가 또는 감소의 방향이 같거나 다름에 따라 양의 상관과 음의 상관이 있습니다. 하지만 회귀성을 나타내는 결정계수는 부호가 항상 양수입니다.
2.3. 공분산(covariance)
집단이나 표본의 공분산은 개체가 가지는 두 확률변수 사이의 관계정보를 가지고 있습니다. 공분산은 개체를 나타내는 점(개체가 가지는 두 변수의 좌표)과 평균점(개체가 가지는 두 변수의 평균을 좌표로 하는 점)이 만드는 두 편차의 곱의 기대값($MM_{XY}$)으로 정의합니다. 따라서 편차제곱과 달리 편차곱은 부호를 가집니다. 집단이나 표본의 공분산은 점(개체, 요소, point, object, element)들의 각 변수값(변량, 데이터값, 데이터수치)과 평균점의 같은 변수와의 편차의 곱의 기대값입니다. 표본의 공분산은 편차곱의 평균입니다. 여기서 각 확률변수의 편차제곱의 기대값은 각 확률변수의 분산입니다. 분산은 항상 0 이상의 실수이지만 공분산은 분산과 달리 음수가 될 수도 있습니다.
모공분산 : 모$\mathrm{Cov}(X{,}Y)=\sigma_{XY}$
$$\sigma_{XY}=\dfrac{\sum\limits_{i=1}\limits^{N}(X_i{-}\mu_{X})(Y_i{-}\mu_{Y})}{N}$$
여기서, $\mu_{X}$는 확률변수 $X$의 모평균
$\mu_{Y}$는 확률변수 $Y$의 모평균
$N$은 집단크기 : 무한집단인 경우 $N → ∞$
표본공분산 : 표본$\mathrm{Cov}(X{,}Y)=S_{XY}$
$$S_{XY}=\dfrac{\sum\limits_{i=1}\limits^{n}(X_i{-}\bar{X})(Y_i{-}\bar{Y})}{n-1}$$
여기서, $\bar{X}$는 확률변수 $X$의 표본평균
$\bar{Y}$는 확률변수 $Y$의 표본평균
$n$은 표본크기
2차원 평면에 표본을 이루는 점을 표시한다고 할때 점은 두개의 변수를 가진다고 할 수 있습니다. 따라서 표본의 평균점을 표시할 수 있고 표본집합의 원소(개체, 요소, element)를 나타내는 점이 분포할 때 공분산은 평균점(mean point, balance point)을 중심으로 하나의 방향으로 모여져 있는가 입니다. 여기서 한 방향성이란 평균점을 중심으로 사사분면으로 나누었을 때 증감의 부호가 같은 1사분면과 3사분면, 그리고 증감의 부호가 다른 2사분면과 4사분면에 퍼져있을 때 같은 방향성을 가진다고 할 수 있습니다. 그리고 표본의 원소가 기울기를 가지는 한 직선상에 모두 위치하는 경우 편차곱의 합이 최대가 되며 두 변수의 표본표준편차의 곱과 같습니다. 사사분면을 나누는 축선에 분포할 때는 편차곱이 0이 되어 공분산도 0이 됩니다.
공분산값은 퍼짐의 방향이 같고 다름에따라 보강 또는 상쇄되어 나타납니다. 평균점을 중심으로 방향에 랜덤하게 골고루 분포하면 공분산은 0이 됩니다. 즉 분포의 방향성이 없다는 것입니다. 사사분면을 나누는 축선과 평행한 직선에 있는 점들은 두 변수가 서로 영향을 미치지 않는 즉, 관계가 없기 때문에 공분산은 0이 됩니다. 반대로 분포가 방향성을 가지고 있는 경우 중에서 가장 방향성이 큰 경우는 점들이 기울기를 가지는 직선 상에 분포할 때 입니다.
2.4. 피어슨상관계수(Pearson correlation coefficient)
공분산이 두 변수의 상관을 표현하기 때문에 공분산을 이용하여 상관계수를 정의합니다. 상관이 가장 큰 경우는 방향을 이루는 경향이 강해서 개체들을 표현한 점들이 평균점을 지나는 한 직선상에 있는 경우입니다. 공분산의 값을 -1과 1사이에 나타내게 하는 방법은 두 변수의 표준편차의 곱으로 나누어 표준화하는 것입니다. 즉, 집단의 모공분산을 두 확률변수의 표준편차의 곱으로 나눈 값을 피어슨 상관계수라 하고 $\rho$(“로”로 읽음)로 표기합니다. 상관계수는 단위가 없는 무차원수입니다.
다시한번 정리하면 두 변수사이가 선형관계가 있다면 이의 정도를 나타내는 비례상수(proportional factor, proportional constant)를 상관계수(correlation efficiency)라 합니다. 또한 상관계수는 표준화된 공분산이라고 할 수 있습니다. 공분산은 각 변수의 단위에 의존하게 되어 변동의 크기를 가늠하기 어려우므로 공분산을 각 변수의 표준편차로 나누어 표준화합니다. 양의 값이면 두 변수가 같은 방향으로 움직이고 음의 값이면 두 변수가 다른 방향으로 움직임을 의미합니다. 상관계수가 0이면 선형관계가 없다는 뜻입니다. 반면 상관계수가 1이나 -1이면 완전한 선형관계를 의미합니다.
확률변수 $X$와 $Y$의 모피어슨상관계수($\rho_{X,Y}$)의 추정량(estimator)은 다음과 같습니다.
$$\rho_{XY}=\dfrac {\sigma_{XY}} {\sigma_{X}\sigma_{Y}}=\dfrac {{\rm E}[(X-\mu_{X})(Y-\mu_{Y})]} {\sigma_X \sigma_Y}=\dfrac{\dfrac{\sum\limits_{i=1}^{N}(X_i-\mu_X)(Y_i-\mu_Y)}{N}} {\sqrt{\dfrac{\sum\limits_{i=1}^{N}(X_i-\mu_X)^2}{N}}\sqrt{\dfrac{\sum\limits_{i=1}^{N}(Y_i-\mu_Y)^2}{N}}}=\dfrac{\sum\limits_{i=1}^{N}(X_i-\mu_X)(Y_i-\mu_Y)}{\sqrt{\sum\limits_{i=1}^{N}(X_i-\mu_X)^2}\sqrt{\sum\limits_{i=1}^{N}(Y_i-\mu_Y)^2}}$$
여기서, $\sigma_{XY}$는 $X$와 $Y$의 모공분산
$\sigma_{X}$는 $X$의 모표준편차
$\sigma_{Y}$는 $Y$의 모표준편차
$\mu_{X}$는 $X$의 모평균
$\mu_{Y}$는 $Y$의 모평균
$N$은 집단크기 : 무한집단인 경우, $N → ∞$
그리고, ${\rm E}[(X-\mu_{X})(Y-\mu_{Y})]={\rm E}[XY]-{\rm E}[X]{\rm E}[Y]$가 성립합니다.
모피어슨상관계수의 예측값($\hat {\rho}$)의 추정량은 아래와 같습니다.
$${\hat {\rho}}_{XY}= \dfrac {S_{XY}} {\sigma_{X}\sigma_{Y}}=\dfrac {{\rm E}\left[{\left({X-\bar {X}}\right)\left({Y-\bar {Y}}\right)}\right]} {\sigma_{X}\sigma_{Y}}=\dfrac{\dfrac{\sum\limits_{i=1}^{n}(X_i-\bar X)(Y_i-\bar Y)}{n-1}} {\sqrt{\dfrac{\sum\limits_{i=1}^{N}(X_i-\mu_X)^2}{N}}\sqrt{\dfrac{\sum\limits_{i=1}^{N}(Y_i-\mu_Y)^2}{N}}}$$
여기서, $S_{XY}$는 $X$와 $Y$의 표본공분산
$\sigma_{X}$는 $X$의 모표준편차
$\sigma_{Y}$는 $Y$의 모표준편차
$S_X$는 $X$의 표본표준편차
$S_Y$는 $Y$의 표본표준편차
$\mu_{X}$는 $X$의 모평균
$\mu_{Y}$는 $Y$의 모평균
$\bar X$는 $X$의 표본평균
$\bar Y$는 $Y$의 표본평균
$N$은 집단크기 : 무한집단인 경우, $N → ∞$
$n$은 표본크기
표본상관계수는 $r$로 표기하며 추정량은 다음과 같습니다. 표본상관계수의 추정량은 모피어슨상관계수의 예측량에서 모분산을 표본분산으로 대체한 경우입니다.
$${r}_{XY}=\dfrac {S_{XY}} {S_{X}S_{Y}}=\dfrac{{\rm E}[(X-\bar X)(Y-\bar Y)]}{S_{X}S_{Y}}=\dfrac{\dfrac{\sum\limits_{i=1}^{n}(X_i-\bar X)(Y_i-\bar Y)}{n-1}} {\sqrt{\dfrac{\sum\limits_{i=1}^{n}(X_i-\bar X)^2}{n-1}}\sqrt{\dfrac{\sum\limits_{i=1}^{n}(Y_i-\bar Y)^2}{n-1}}}=\dfrac{\sum\limits_{i=1}^{n}(X_i-\bar X)(Y_i-\bar Y)}{\sqrt{\sum\limits_{i=1}^{n}(X_i-\bar X)^2}\sqrt{\sum\limits_{i=1}^{n}(Y_i-\bar Y)^2}}$$
여기서, $S_{XY}$는 $X$와 $Y$의 표본공분산
$S_X$는 $X$의 표본표준편차
$S_Y$는 $Y$의 표본표준편차
$\bar X$는 $X$의 표본평균
$\bar Y$는 $Y$의 표본평균
$n$은 표본크기
2.5. 표본피어슨상관계수의 표준오차
표본피어슨상관계수의 표준오차($\mathrm{SE}(r)$)는 표본피어슨상관계수($r$) 표집의 표준편차와 같으며 다음과 같습니다.
$$\mathrm {SE}(r)=\sigma_r=\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}$$
여기서, $\sigma_r$은 표본피어슨상관계수 표집의 표준편차
$n$은 표본크기
표본피어슨상관게수의 표준오차는 표본피어슨상관계수와 모피어슨상관계수와 차이의 기대값입니다.
$$\mathrm {SE}(r)={\rm E}[r-\rho]=\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}$$
여기서, $r$은 표본피어슨상관계수
$\rho$는 모피어슨상관계수
$n$은 표본크기
표본피어슨상관계수의 표준오차 유도
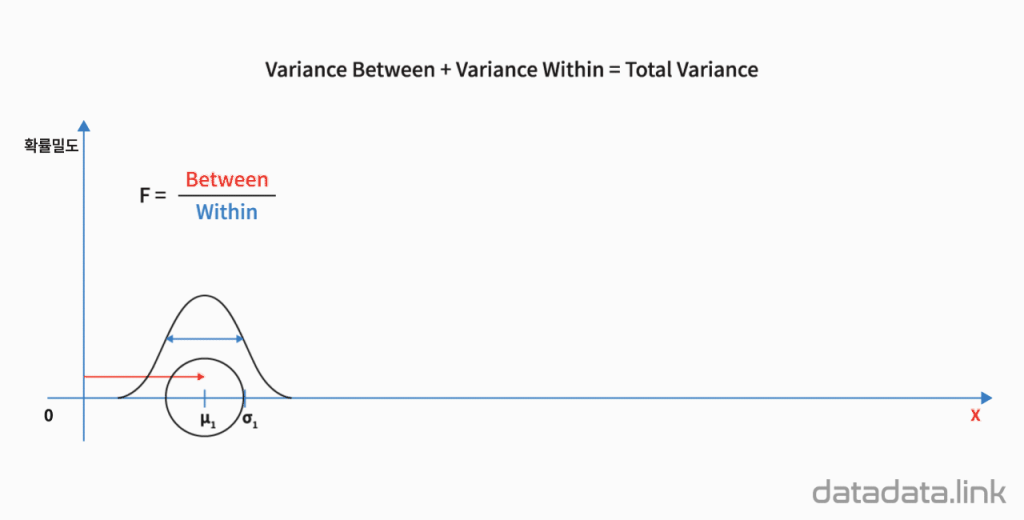
분산분석에서 회귀정도를 나타내는 새로운 확률변수 $F$는 다음과 같습니다.
$$F=\dfrac{MS_{Reg}}{MS_{Res}}=\dfrac{\dfrac{SS_{Reg}}{k-1}}{\dfrac{SS_{Res}}{n-k}}$$
여기서, $k$는 수준수
$n$은 표본크기
두 변수의 상관에서는 상관이 있는 집단과 상관이 없는 집단으로 구분할 수 있습니다. 그래서, 위식의 분산분석에서의 집단의 수인 $k$를 2로 놓을 수 있습니다. 따라서 새로운 확률변수인 $F$는 상관분석에서는 다음식과 같습니다.
$$F=\dfrac{MS_{Reg}}{MS_{Res}}=\dfrac{\dfrac{SS_{Reg}}{2-1}}{\dfrac{SS_{Res}}{n-2}}$$
여기서, $n$은 표본크기
피어슨상관계수가 회귀직선으로의 회귀정도를 나타내므로 피어슨상관계수와 새로운 확률변수 $F$의 관계를 구할 수 있습니다. 결정계수($R^2$)의 정의는 다음과 같습니다.
$$R^2=\dfrac{SS_{Reg}}{SS_T}=\dfrac{SS_{Reg}}{SS_{Reg}+SS_{Res}}$$
여기서, $SS_{Reg}$는 회귀제곱합
$SS_{Res}$는 잔차제곱합
$SS_T$는 총제곱합
결정계수식을 변형하면 다음식과 같습니다.
$$\dfrac{1}{R^2}=1+\dfrac{SS_{Res}}{SS_{Reg}}=1+\dfrac{(n-2)MS_{Res}}{MS_{Reg}}$$
여기서, $MS_{Res}$는 잔차제곱합의 평균
$MS_{Reg}$는 회귀제곱합의 평균
$n$은 표본크기
따라서, 결정계수($R^2$)와 새로운 확률변수($F$)의 관계식을 아래와 같이 구할 수 있습니다.
$$1=R^2+(n-2)R^2\dfrac{1}{F}$$
위식을 정리하면
$$F=(n-2)\dfrac{R^2}{1-R^2}$$
여기서, $n$은 표본크기
$R^2$은 결정계수
두 변수의 표본피어슨상관계수의 제곱($r^2$)은 두 변수를 가지는 개체로 이루어진 표본의 결정계수($R^2$)와 같습니다. 따라서, 새로운 확률변수, $F$를 상관계수로 표현하면 다음식과 같습니다.
$$F=(n-2)\dfrac{r^2}{1-r^2}$$
여기서, $n$은 표본크기
$r$은 표본피어슨상관계수
새로운 확률변수인 $t$로 정리하면
$$t=\sqrt{(n-2)\dfrac{r^2}{1-r^2}}=\dfrac{r}{\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}}=\dfrac{r}{{\rm SE}(r)}$$
여기서, $n$은 표본크기
$r$은 표본피어슨상관계수
2.6. 설명강의
– 준비 중

3. 실습
3.2. 구글시트 함수
=AVERAGE(C3:C22) : 평균. C3에서 C22에 있는 데이터의 평균. 데이터를 모두 더한 후, 데이터의 개수로 나눈 산술평균.
3.3. 실습강의
– 준비중

4. 용어와 수식
4.1 용어
결정계수(coefficient of determination)
변동계수(Coefficient of variation), 상관계수(Coefficient of correlation)와 혼동하기 쉽습니다. 통계에서, 결정계수(coefficient of determination: R2 ,r2로 표현되며 R squared로 읽음) 는 독립변수들로부터 예측이 가능한 종속변수가 가지는 분산의 확률(예측이 가능하지 않은 종속변수와 상대비율)입니다.
통계적 모형(statistical models)에서 주로 사용되는 통계로써, 관련 정보를 통한 가설의 증명이나 미래의 일을 예상하는 데에 주로 사용됩니다. 결정계수는 통계적 모델로 표현된 결과의 전체 변동 비율에 따라 모델이 관찰된 결과를 얼마나 잘 반영했는지에 대한 수치를 제공합니다.
결정계수, $R^2$는 여러 정의가 존재합니다. 한 종류로는 $R^2$ 대신에 쓰여지는 $r^2$로 단순선형회귀(simple linear regression)가 있습니다. 절편(intercept)이 포함된 경우에는 관측된 결과와 예측값 사이의 표본상관계수($r$, correlation coefficient)의 제곱입니다. 회귀분석기(regressors)가 포함된 경우, R2는 다중상관계수(coefficient of multiple correlation)의 제곱입니다. 두 경우 모두, 결정계수는 0에서 1 사이입니다.
정의에 따라 $r^2$이 음수가 될 수 있습니다. 이는 해당 결과에 대한 예측이 모형(model)의 적합한 방식으로 도출되지 않았을 때에 발생할 수 있습니다. 또는 모형의 적합한 방식이 사용되더라도 여전히 음수일 수도 있습니다. 예를 들어, 절편을 포함하지 않고 선형회귀를 수행하거나, 데이터를 위해 비선형 함수를 사용할 경우에 음수가 될 수 있습니다. 음수가 되었다는 것은 특정 기준에 따라 데이터의 평균이 적합 함수값보다 더 적합하다는 뜻입니다. 결정계수의 가장 일반적인 정의는 “내쉬-서트클리프 모형 효율 계수(Nash–Sutcliffe model efficiency coefficient) “로도 알려져 있고, 이 표기법은 제곱기호가 있어서 혼동이 되기는 하지만 음의 값을 가지는 -∞에서 1까지의 범위를 가지는 적합도 지표를 나타내고 많은 분야에서 선호됩니다.
시뮬레이션값($Y_{pred}$)과 측정값($Y_{obs}$)의 적합도(the goodness-of-fit)를 평가할 때 선형회귀의 선형계수($R^2$)를 기반으로 하는 것은 적절하지 않습니다(i.e., $Y_{obs}= mY_{pred} + b$). 선형계수는 시뮬레이션값과 측정값의 선형 상관정도를 정량화하는 반면에, 적합도 평가의 경우에는 하나의 특정 선형 상관관계($Y_{obs}= Y_{pred} + b$ : the 1:1 line)만 고려해야 합니다.
Reference
Coefficient of determination – Wikipedia