회귀평면의 적합성 – 회귀계수 : 중선형회귀분석 t검정
1. 애니메이션
2. 설명
2.1 적용 예
원인변수가 2개인 경우
2.2. 중선형회귀모형
$$Y_i=\beta_o+\beta_1 X_{i1}+\cdots+\beta_k X_{ik}+\epsilon_i$$
여기서, $n$은 표본크기
$$Y=X\beta+\epsilon$$
$$
Y=
\begin{bmatrix}
Y_1 \\
Y_2 \\
\vdots \\
Y_n
\end{bmatrix},
X=
\begin{bmatrix}
1 & X_{11} & X_{12} & \cdots & X_{1k} \\
1 & X_{21} & X_{22} & \cdots & X_{2k} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & X_{n1} & X_{n2} & \cdots & X_{nk}
\end{bmatrix},
\beta=
\begin{bmatrix}
\beta_0 \\
\beta_1 \\
\vdots \\
\beta_k
\end{bmatrix},
\epsilon=
\begin{bmatrix}
\varepsilon_1 \\
\varepsilon_2 \\
\vdots \\
\epsilon_n
\end{bmatrix}
$$
2.3. 중선형회귀분석
제곱합과 자유도의 분할
제곱합 등식
$$SS_T=SS_{Reg}+SS_{Res}$$
자유도 등식
$$n-1=p+(n-p-1)$$
여기서, $n$은 표본크기
$p$는 원인변수 개수
잔차제곱합 : $SS_{Res}$
$$SS_{Res}=\sum\limits_{i=1}^{n}{\epsilon_i}^2=\epsilon^{\prime}\epsilon=(Y-X\beta)^{\prime}(Y-X\beta)$$
여기서, $n$은 표본크기
잔차분석
잔차
$$e_i=Y_i-\hat{Y}_i=Y_i-(b_0+b_1 X_{i1}+\cdots +b_k X_{ik})$$
잔차벡터
$$\bf{e}=\bf{Y}-\bf{X{\beta_1}}$$
잔차표준오차
$$\mathrm{SE}(Residual)=\sqrt{\dfrac{1}{n-p-1}\sum\limits_{i=1}^{n}(Y_i-\hat{Y}_i)^2}$$
여기서, $p$는 원인변수의 수
$n$은 표본크기
중선형회귀분석표
$$\hat{\beta_i}\sim\mathrm{N}(\beta_i,c_{ii}\cdot \sigma^2)$$
여기서, $i=0,1,\cdots,p$
중선형회귀분석표
| 제곱합 (sum of squared) |
자유도 (degrees of freedom) |
제곱평균 (mean of squared) |
검정통계량 (test statistic) |
|
| 회귀 (Regression) |
$SS_{Reg}$ | $p$ | ${MS}_{Reg}=\dfrac{SS_{Reg}}{p}$ | $F=\dfrac{MS_{Reg}}{MS_{Res}}$ |
| 잔차 (Residual) |
$SS_{Res}$ | $n-p-1$ | $MS_{Res}=\dfrac{SS_{Res}}{n-p-1}$ | |
| 총 (Total) |
$SS_T$ | $n-1$ | $MS_T=\dfrac{SS_T}{n-1}$ |
2.4 중선형회귀분석 : 모회귀계수($\beta_i$) 추정
모회귀계수 점추정량
$$\hat{\beta_i}$$
표본회귀계수의 표준오차
$${\rm SE}(\hat{\beta_i})=\sqrt{c_{ii}}\cdot {\bf S}$$
모회귀계수 신뢰구간
$${\beta_i}=\hat{\beta_i}\pm t_{n-k-1;\frac{\alpha}{2}} {\rm SE}(\hat{\beta_i})$$
여기서, $ t_{n-k-1;\frac{\alpha}{2}}$는 유의수준($\alpha$)에서 임계값
2.5. 중선형회귀분석 : 모회귀계수 $t$검정
귀무가설
$$H_0: \bf{\beta_i}=\bf{\beta_{i,0}}$$
검정통계량
$$t=\dfrac{\bf{\hat{\beta_i}}-\bf{\beta_{i,0}}}{\mathrm{SE}(\bf{\hat{\beta_i}})}$$
귀무가설 기각역
대립가설이 $H_1: \beta_i\lt\beta_{i0}$ 이면 $t\lt -t_{n-k-1;\alpha}$
대립가설이 $H_1: \beta_i\gt\beta_{i0}$ 이면 $t\gt t_{n-k-1;\alpha}$
대립가설이 $H_1: \beta_i\ne\beta_{i0}$ 이면 $\left|t\right|\gt t_{n-k-1;\frac{\alpha}{2}}$
중선형회귀분석 회귀계수 $t$검정표
| 귀무가설$(H_0)$ | 검정통계량의 값 | 대립가설$(H_1)$ | 귀무가설 기각역 |
| $ \beta_i=\beta_{i0}$ | $t=\dfrac{\hat{\beta_i}-\beta_{i0}}{\mathrm{SE}(\hat{\beta_i})}$ | $ \beta_i\lt\beta_{i0}$ | $t\lt -t_{n-k-1;\alpha}$ |
| $ \beta_i\gt\beta_{i0}$ | $t\gt t_{n-k-1;\alpha}$ | ||
| $ \beta_i\ne\beta_{i0}$ | $\left|t\right|\gt t_{n-k-1;\frac{\alpha}{2}}$ |
3. 실습
3.2. 구글시트 함수
=COUNT(F3:F22) : 데이터 개수. F3에서 F22에 있는 숫자로 표시된 데이터의 개수.
=AVERAGE(F3:F22) : 평균. F3에서 F22에 있는 데이터의 평균.
=VAR.S(C3:C22) : 표본분산. F3에서 F22에 있는 데이터의 표본분산. 편차제곱합을 데이터 개수 -1로 나눔.
=STDEV.S(F3:F22) : 표본표준편차. F3에서 F22에 있는 데이터의 표본표준편차. 표본분산의 제곱근.
=T.DIST.2T(O3,P3) : t분포 상에서 확률변수의 양측 확률밀도. O3 확률변수에 대해 P3를 자유도로 하는 t분포 상에서의 양측 확률밀도를 계산해서 구함.
=T.INV(1-(T3/U3),H3-1) : 확률밀도에 해당하는 확률변수를 구함. H3-1을 자유도로 가지는 t분포 상에서 1-(T3/U3)의 누적확률밀도로 하는 확률변수 값을 표시함.
=IF(S3>V3,”YES”,”NO”) : 조건문, S3의 값이 V3보다 크면 YES를 표시하고, 그렇지 않으면 NO를 표시함.
3.3. 실습강의
– 가설
– 확률변수
– 가설검정
– 실습 안내
4. 수식과 용어
4.1 용어
자유도
통계에서 자유도는 통계의 최종 산출과정에서 사용되는 변할 수 있는 값들의 갯수입니다.
한편, 동적 계(시스템)가 움직일 수 있는 독립적인 방법의 수도 자유도라 합니다. 즉, 동적 계(시스템)에서의 자유도는 시스템의 상태를 확정 지을수 있는 최소의 독립 좌표수라고 정의할 수 있습니다. 예를 들면, 3차원 공간에서의 계의 운동은 6자유도로 표현합니다. 즉, 선운동의 방향 3자유도와 원운동의 방향 3자유도로 표현합니다. 계의 위치도 마찬가지로 6자유도입니다. 계의 공간에서의 위치를 지정하는 3개의 좌표와 계의 방향을 지정하는 방향벡터는 3개의 좌표를 가지고 있습니다.
통계의 모수(매개변수, parameter)값은 정보나 데이터의 양에 따라 달라집니다. 모수의 추정에 들어가는 독립적인 정보의 수를 통계에서는 자유도라 부릅니다. 일반적으로, 자유도는 모수의 추정에 들어간 독립변수들의 수에서 모수의 추정에서 중간 단계로 사용된 모수의 수를 뺀 값입니다. 예를 들면, 표본분산은 표본크기($n$ )로 표현되는 개수의 확률변수들로부터 1번의 연산을 거친 모수인 표본평균에서의 거리로 구하기 때문에 표본분산은 표본평균의 갯수 1을 뺸 $(n-1)$의 자유도를 가집니다.
수학적으로, 자유도는 확률변수 또는 확률벡터의 차원 수, 또는 본질적으로는 “자유로운” 구성 요소의 수로 볼 수 있습니다. 이 용어는 특정 임의 벡터가 선형 부분 공간에 속하도록 제한되어 있고 자유도가 공간의 차원을 나타내어 선형모델(선형회귀 분석, 분산분석)에 주로 사용됩니다. 자유도는 또한 벡터의 제곱 크기(좌표의 제곱합)와 연관된 통계에서 나타나는 카이제곱 및 기타 분포의 모수(매개변수, parameter)와 관련됩니다.
Reference
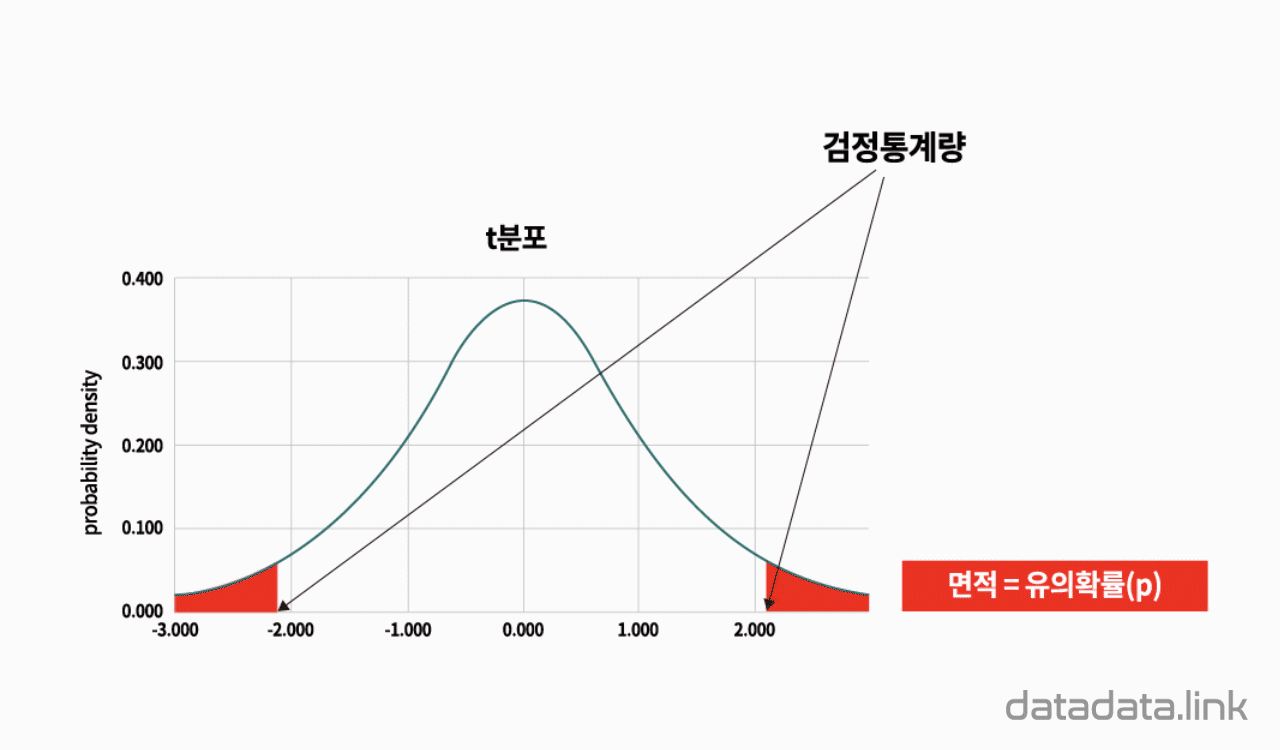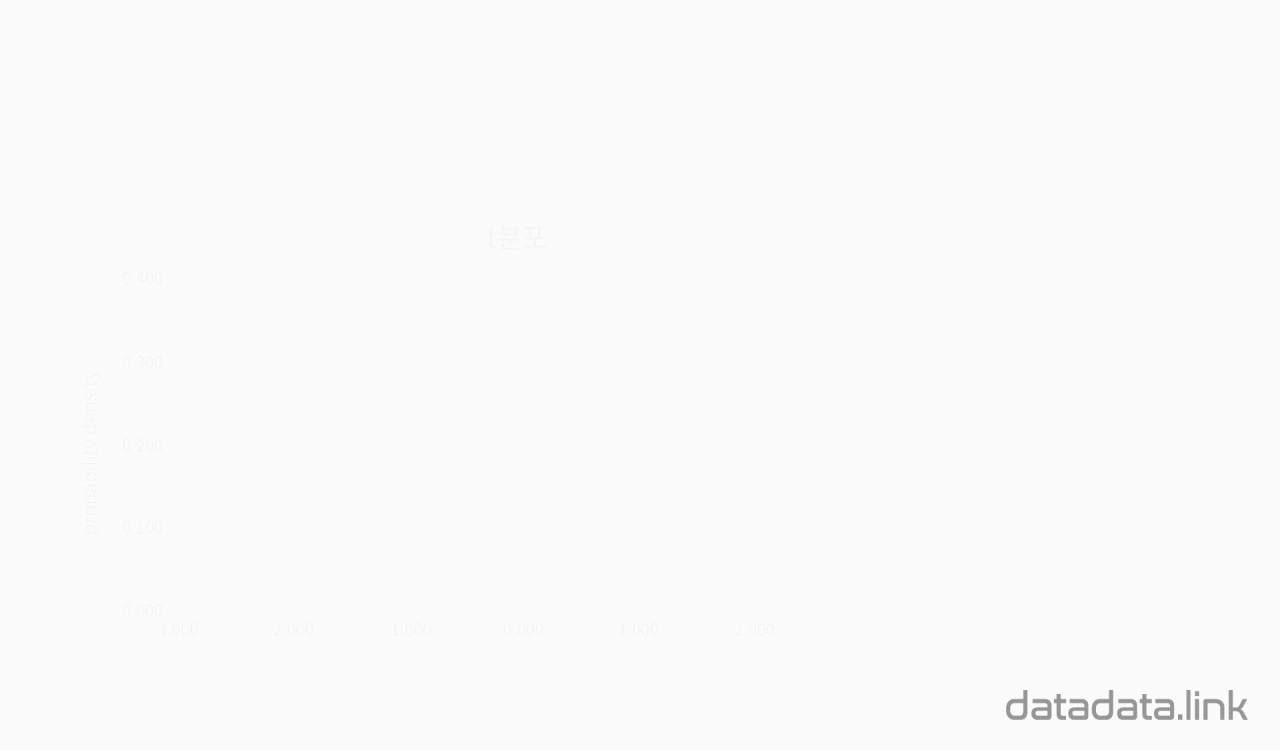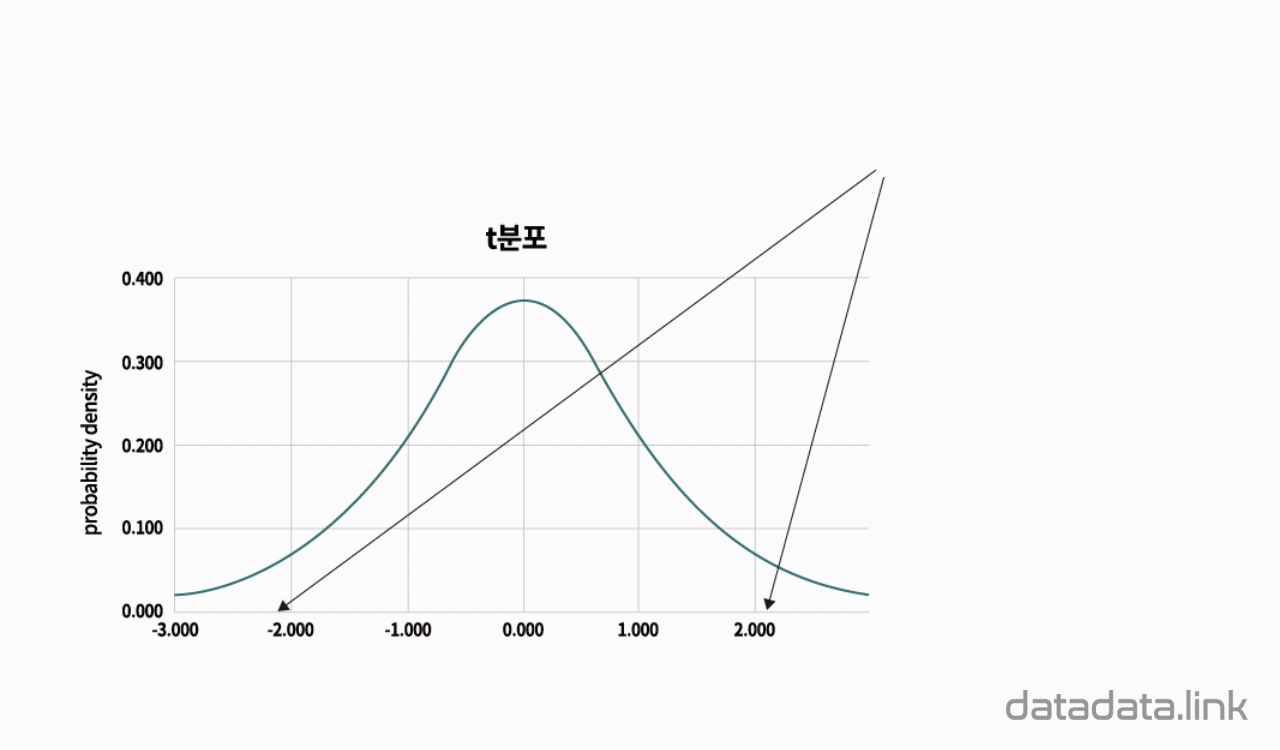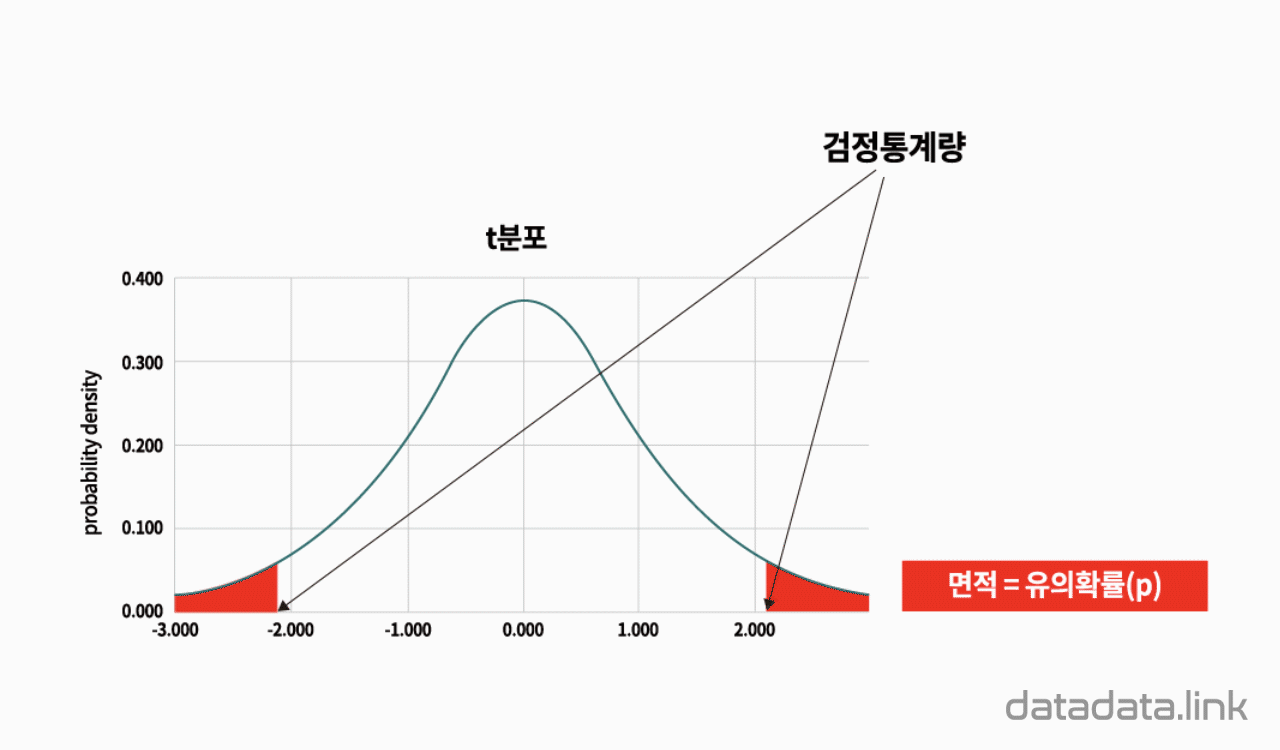
$p$값($p$-value, Probability value)
통계의 가설검정에서 $p$값(확률값)은 주어진 통계모델에 대하여 귀무가설이 참일 때 비교된 두 집단 간의 표본평균 차이의 절대값이 실제 관측값보다 크거나 같을 확률입니다. $p$값은 물리학, 경제학, 금융학, 인문학, 심리학, 생물학, 법학 및 사회과학과 같은 많은 분야의 연구에서 일반적으로 사용됩니다.