결과변수 예측 – 변수 3개이상 : 중선형회귀모형

예측(forecast, prediction)

미래의 특정시점에서 설명변수(독립변수)의 값을 알 때 종속변수의 값을 예측하는 수요는 특히 계량경제학의 중요한 부분입니다. 예측은 두 변수가 인과관계에 의한 함수관계(선형)를 갖고 있을 때 표본회귀선에 의거하여 미래의 종속변수값을 판정하는 것입니다.

추정의 결과인 회귀선이 적합도나 통계적 유의검정에서 바람직한 것으로 평가되면 이를 바탕으로 미래를 예측할 수 있게 됩니다. 예측의 시기에 따라 사후적 예측(post forecast)과 사전적 예측(ante forecast)으로 구분합니다.

1) 사후적 예측(사후적 평가 : 머신러닝)

예측한 시각이 회귀분석 완료 시각 이후에 속하더라도 이미 과거에 속한 시각이라면 비록 설명변수와 종속변수의 값을 알고 있다 하더라도 다시 설명변수 값을 표본회귀선에 대입하여 종속변수를 구하는 것입니다. 이러한 사후적 예측과정은 예측자체보다는 추정된 표본회귀선에 의해 예측된 종속변수 값이 실제 실현된 종속변수 값과 얼마나 근접된 값으로 나타나는지 확인함을 써 표본회귀선의 효용성을 평가하는 방법으로 이용할 수 있습니다.

2) 사전적 예측

현시점이후에 속하는 미래를 대상으로 하되 가정된 설명변수(독립변수) 값을 가지고 종속변수 값을 추정하는 것입니다. 미래에 대한 예측을 시행할 때 설명변수(독립변수)의 값이 알려져 있는 지의 여부가 중요한 역할을 합니다. 현실적으로 주로 사용하는 예측방법은 사전적 예측에 속하나 설명변수 값이 알려져 있다는 가정하에 무조건부 예측을 주로 사용합니다.

조건부 예측(conditional forecast): 설명변수가 미지인 상태에서의 예측으로 사전적 예측이 이에 속합니다.

무조건부 예측(unconditional forecast): 설명변수가 알려진 상태에서의 예측으로 사후적 예측이 주로 이에 속합니다. 무조건부 예측은 크게 점예측(point forecast)과 구간예측(interval forecast)의 두가지가 있습니다

점예측 : 단순히 표본관측점들을 근거로 최소제곱법에 의해 도출된 표본회귀선을 이용하여 가상적인 미래의 설명변수값 $X_f$ (단, 이 $X$ 값은 표본회귀선 도출을 위한 회귀분석에사용되지 않은 별도의 $X$ 값) 에 대응하는 종속변수값을 하나의 수치로 표현하는 방법입니다.

추정된 회귀선이 $Y_i=\hat{\beta_0}+\hat{\beta_1}X_i$ 이라하면, 새로운 관찰값 $f $의 설명변수값, $X_f$를 알 때 $Y_f $의 예측치 (predicted value)는 다음과 같습니다.

$\hat{Y_f}= \hat{\beta_0}+\hat{\beta_1}X_f$

예측오차(prediction error)인 $e_f =\hat{Y_f}-Y_f$는 다음과 같은 특성을 갖습니다. 만일 오차항 분산값($\sigma^2$)이 알려져 있지 않을 경우에는 추정치 $s^2$를 이용합니다.

$\mathrm{E}(e_{f}) = 0$

${\mathrm{Var}}{(}{e}_{f}{)}{=}{\mathit{\sigma}}^{2}{[}{1}{+}{(}\frac{1}{n}{)}{+}{\{}\frac{{(}{X}_{f}{-}{X}{)}^{2}}{\mathop{\sum}\limits_{}\limits^{}{{(}{X}_{i}{-}{X}{)}^{2}}}{\}]}$

${\mathrm{Var}}{(}\hat{e}{)}{=}{\mathit{\sigma}}^{2}{[}{1}{+}{(}\frac{1}{n}{)}{+}{\{}\frac{{(}{X}_{f}{-}{X}{)}^{2}}{\mathop{\sum}\limits_{}\limits^{}{{(}{X}_{i}{-}{X}{)}^{2}}}{\}]}$

$\frac{{e}_{f}}{{s}_{f}{}^{2}}{=}\frac{{(}{\hat{Y}}_{f}{-}{Y}_{f}{)}}{{s}_{f}{}^{2}\sim{t}{(}{n}{-}{2}{)}}$

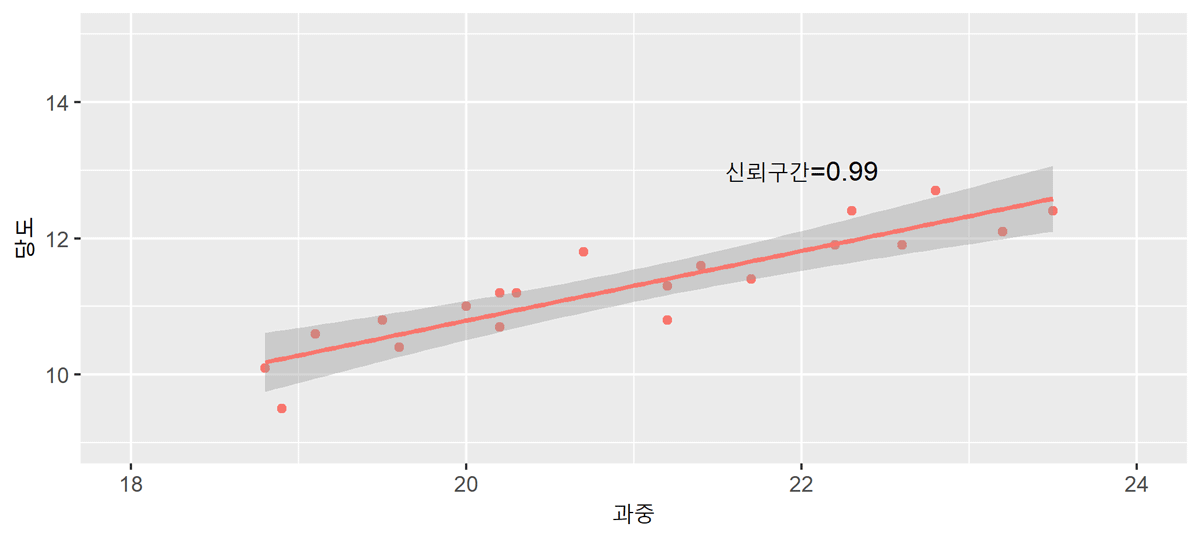
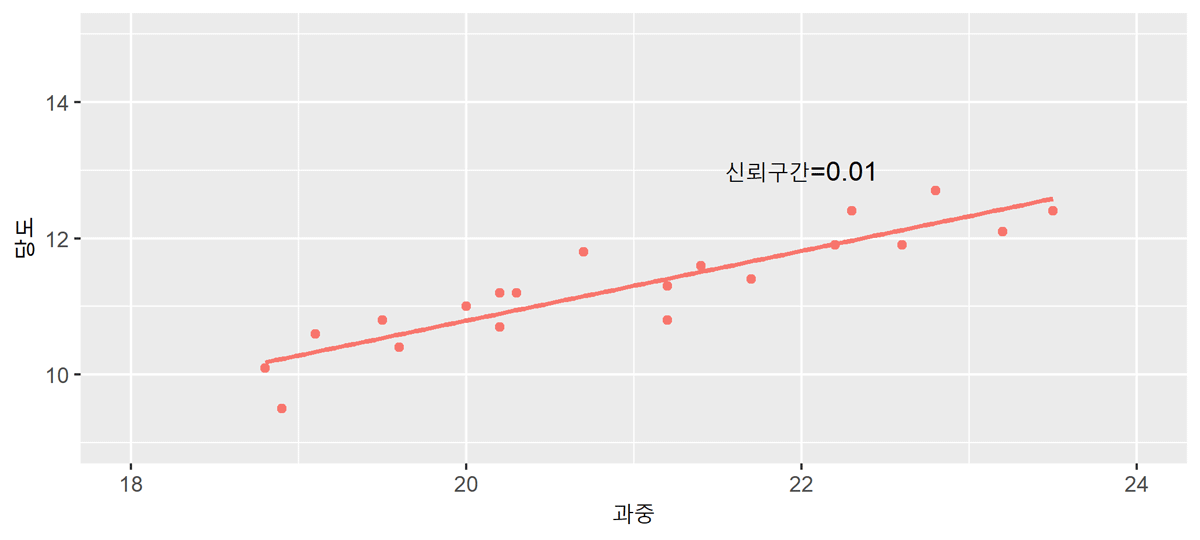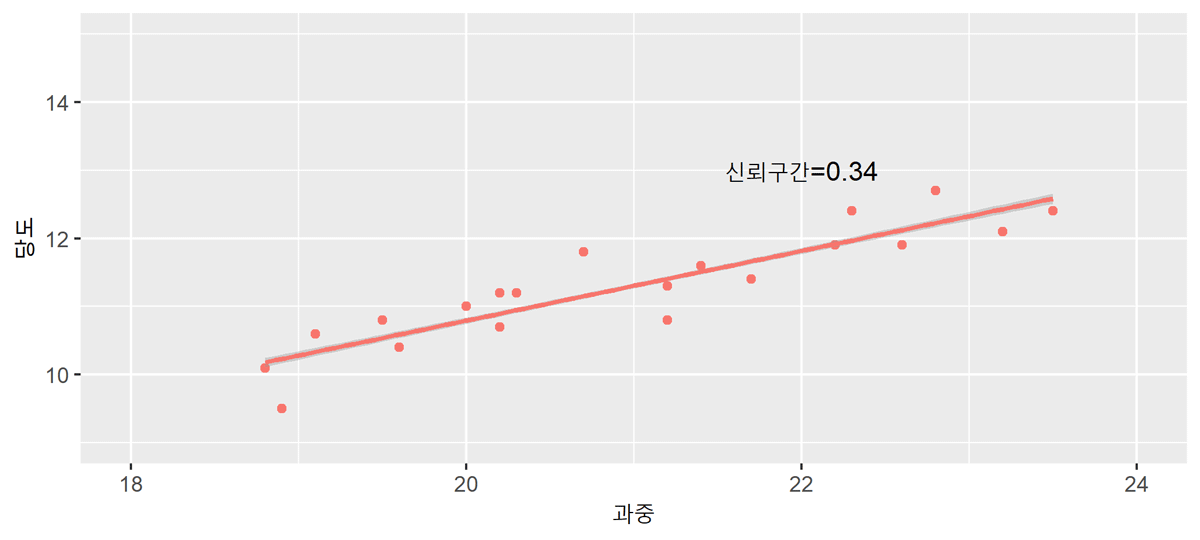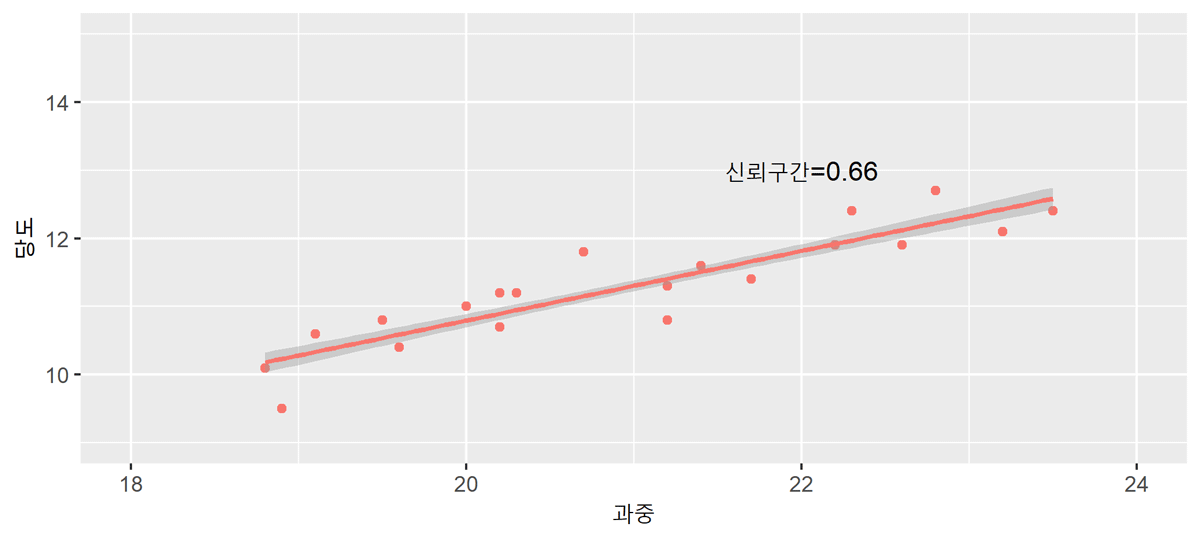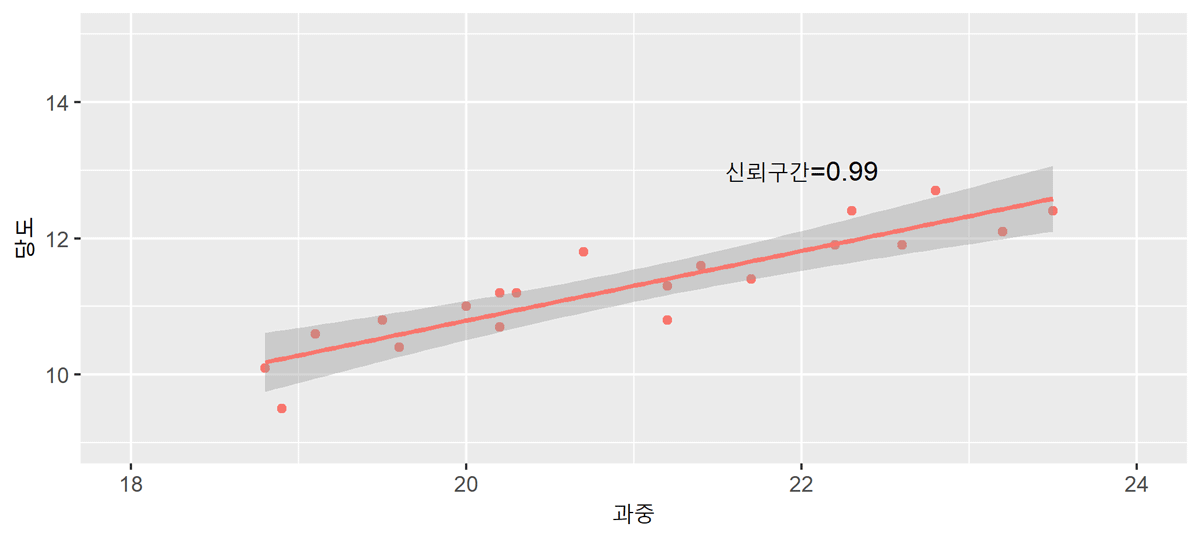
구간 예측

점예측의 경우 아무리 가까운 미래에 대한 예측이라 하더라도 점예측값과 실제 종속변수값이 일치할 가능성은 희박합니다. 따라서 이러한 점예측치를 중심으로 일정한 구간을 설정하여 제시하는 구간예측을 동시에 실시합니다.

실제 $Y_f$에 대한 $100(1-\alpha)%$ 신뢰구간예측은

${[}{Y}_{f}\pm{t}{(}\frac{\beta_0}{2}{)}{s}_{f}{]}$

예측에 있어서 관찰 표본의 수($n$)이 클수록 예측오차의 분산이 작아지고 일정한 신뢰수준 하에서 신뢰구간이 좁아지게 되어 정확한 예측치를 얻을 수 있습니다. 예측하고자 하는 $X_f$ 값이 평균값($\bar{X}$)과 멀어질수록 예측오차는 커지고 예측구간 폭은 점차 넓어지므로 예측의 신뢰성이 낮아집니다.